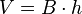QUE ES ESCUELA AL REVEZ
AMI- Una revolución educativa que ya está en marcha en Estados Unidos podría extenderse muy pronto a América latina: se trata de las "clases al revés", en que los estudiantes estudian en casa y hacen sus tareas en la escuela con la ayuda de sus maestros.
La Khan Academy, un sitio web sin fines de lucro con videos gratuitos y ejercicios interactivos para estudiantes, ya tiene alrededor de 60 millones de visitantes únicos anuales, y acaba de lanzar su sitio en español (es.khanacademy.org). Ofrece más de 800 videos en español para ayudar a los niños a estudiar sus clases de matemática y varias otras materias, gratis y sin publicidad.
La semana pasada entrevisté a Salman Khan, de 37 años, fundador de la Khan Academy. A juzgar por lo que ha logrado, no me extraña que la revista Time lo haya nombrado una de las 100 personas más influyentes del mundo. Su historia es asombrosa. Después de obtener cuatro títulos universitarios del Instituto de Tecnología de Massachusetts (MIT) y Harvard, Khan empezó a trabajar en un fondo de inversiones de Boston. Por las noches, a menudo ayudaba por teléfono a su prima Nadia, que tenía 11 años y vivía en Nueva Orleáns, a hacer sus tareas de matemáticas.
POLIEDROS:
Un poliedro es, en el sentido dado por la geometría clásica al término, un cuerpo geométrico cuyas caras son planas y encierran un volumen finito. La palabra poliedro viene del griego clásico πολύεδρον (polyedron), de la raíz πολύς (polys), "muchas" y de έδρα (edra), "base", "asiento", "cara".
Los poliedros se conciben como cuerpos tridimensionales, pero hay semejantes topológicos del concepto en cualquier dimensión. Así, el punto o vértice es el semejante topológico del poliedro en cero dimensiones, una arista o segmento lo es en 1 dimensión, el polígono para 2 dimensiones; y el polícoro el de cuatro dimensiones. Todas estas formas son conocidas como politopos, por lo que podemos definir un poliedro como un polítopo tridimensional.

Clasificación según el número de caras[editar]
| Nombre | Número de caras |
|---|---|
| tetraedro | 4 |
| pentaedro | 5 |
| hexaedro | 6 |
| heptaedro | 7 |
| octaedro u octoedro | 8 |
| eneaedro o nonaedro | 9 |
| decaedro | 10 |
| endecaedro o undecaedro | 11 |
| dodecaedro | 12 |
| tridecaedro | 13 |
| tetradecaedro o tetracaidecaedro | 14 |
| pentadecaedro o pentedecaedro | 15 |
| hexadecaedro | 16 |
| heptadecaedro | 17 |
| octadecaedro u octodecaedro | 18 |
| eneadecaedro o nonadecaedro | 19 |
| icosaedro o isodecaedro | 20 |
| triacontaedro | 30 |
| tetracontaedro | 40 |
| pentacontaedro | 50 |
| hexacontaedro | 60 |
| heptacontaedro | 70 |
| octacontaedro u octocontaedro | 80 |
| eneacontaedro o nonacontaedro | 90 |
| hectaedro | 100 |
| chiliedro | 1000 |
| miriedro | 10000 |
| decemiriedro | 100000 |
| hectamiriedro o megaedro | 1000000 |
| apeiroedro | ∞ |
a) Tetraedro Regular:
b) Hexaedro Regular:

c) Octaedro Regular:

d) Dodecaedro Regular

e) Icosaedro Regular

ÁREA:
VOLUMEN:
Para otros usos de este término, véase Prisma.
En geometría, un prisma es un poliedro con una base poligonal de n lados, una copia de traslación (no en el mismo plano que la primera), y otras n caras (todas necesariamente deben ser paralelogramos) que une los lados correspondientes de las dos bases. Todas las secciones transversales paralelas a las caras de la base son iguales. Los prismas se nombran para su base, por lo que un prisma de base pentagonal se llama un prisma pentagonal. Los prismas son una subclase de los prismatoides
| Prisma | ||
|---|---|---|
 Imagen del sólido | ||
| Caras | 2+n total: 2 {n} n {4} | |
| Aristas | 3n | |
| Vértices | 2n | |
| Grupo de simetría | Dnh | |
| Poliedro dual | Bipirámide n-gonal | |
| Propiedades | ||
| Poliedro convexo,semi-regular | ||
| Plano | ||
 | ||
| [editar datos en Wikidata] | ||
Volumen[editar]
El volumen de un prisma es el producto del área de la base y la distancia entre las dos caras de base, o la altura (en el caso de un prisma no derecho, tener en cuenta que esto significa la distancia perpendicular).
Por consiguiente, el volumen es:
donde B es el área de la base y h es la altura. Por lo tanto, el volumen de un prisma, cuya base es un polígono regular de n lados con una longitud de lado s, es:

- Los prismas son cuerpos poliedros que poseen 2 caras basales iguales, paralelas y poligonales (triángulo, cuadrilátero, pentágono...) y tantas caras laterales rectangulares como lados tiene el polígono de sus caras basales.
- Características
La altura de un prisma es la distancia entre las bases.
Si todas las caras laterales son rectángulos, serán perpendiculares a las bases y entonces se llama prisma recto.
Si la caras laterales no son perpendiculares a las bases, se llama prisma oblicuo.
Las aristas laterales de un prisma son segmentos iguales y paralelos entre si. En los prismas rectos son perpendiculares a las bases.
Prismas y pirámides
- ÍNDICE DE TEMAS:
- Prismas
- Pirámides
Prismas
Prismas rectosLos prismas rectos son aquellos cuyas aristas laterales son perpendiculares a las bases.- Prismas de base triangular: posee 5 caras, 9 aristas y 6 vértices. Sus caras basales corresponden a triángulos.- Prismas de base cuadrangular: posee 6 caras, 12 aristas y 8 vértices.* Cubo: prisma que posee 6 caras cuadradas e iguales, 12 aristas y 8 vértices.* Prisma de base rectangular: posee 6 caras, 12 aristas y 8 vértices. Sus caras basales corresponden a rectángulos.- Prisma de base pentagonal: posee 7 caras, 15 aristas y 10 vértices. Sus caras basales corresponden a pentágonos.Como puedes observar, los prismas son cuerpos geométricos formados por líneas rectas.
Ejemplos
Calcular el área lateral, el área total y el volumen de un tronco de cono de radios 6 y 2 cm, y de altura 10 cm.
El cono, el cilindro y la esfera
Estos tres cuerpos se generan al hacer girar una línea alrededor de un eje. La línea que gira recibe el nombre de generatriz y los puntos que ella describe forman una circunferencia.
El cono
Es el cuerpo geométrico redondo que se obtiene al girar una recta oblicua desde un punto fijo del eje. A ese punto se le llamacúspide. La recta, llamada generatriz, gira a lo largo de una circunferencia, directriz, que se encuentra en otro plano.
Otra forma más sencilla de determinar la formación de un cono es decir que se genera al rotar un triángulo rectángulo alrededor de uno de sus catetos.
Elementos de un cono recto
- Eje: es el cateto AC. Alrededor de él gira el triángulo rectángulo.
- Base: es el círculo que genera la rotación del otro cateto, AB. Por lo tanto, AB es el radio del cono. La base se simboliza: O (A, AB)
- Generatriz: es la hipotenusa del triángulo rectángulo, BC, que genera la región lateral conocida como manto del cono.
- Altura: corresponde al eje del cono, porque une el centro del círculo con la cúspide siendo perpendicular a la base.
Observa los elementos del cono recto en este esquema:
El cono tiene una cara basal plana y una cara lateral curva. Posee una arista basal y un vértice llamado cúspide.
Cono recto y cono oblicuo
Si la altura coincide con su eje, el cono es recto. Si el eje y la altura no coinciden, el cono es oblicuo.
Red del cono
Al abrir un cono obtenemos su red, es decir, la plantilla dibujada en un mismo plano para poder construirlo.
La cara lateral o manto de un cono corresponde a un sector circular.
Llamamos sector circular a una parte del círculo formado por 2 radios y el arco de circunferencia comprendido entre ellos.
Llamamos sector circular a una parte del círculo formado por 2 radios y el arco de circunferencia comprendido entre ellos.
En el manto del cono, los radios son la generatriz, y el arco equivale al perímetro de la circunferencia basal.
El cilindro
Este cuerpo redondo se forma con todas las rectas paralelas que cortan a 2 circunferencias congruentes ubicadas en planos paralelos.
Nuevamente obtendremos, de forma más sencilla, la formación de un cilindro recto. Haremos girar un rectángulo alrededor de uno de sus lados.
Elementos de un cilindro recto
- Eje: lado AD, alrededor del cual gira el rectángulo
- Bases: son los círculos paralelos y congruentes que se generan al girar los lados AB y CD del rectángulo. Cada uno de estos lados es el radio de su círculo y también, el radio del cilindro.
- Altura: corresponde al mismo eje AD, es perpendicular a las bases y llega al centro de ellas. Esta es la razón por la que el cilindro es recto.
- Generatriz: es el lado BC, congruente con el lado AD, y que al girar forma la cara lateral o manto del cilindro.
Observa los elementos del cilindro en este esquema:
El cilindro tiene 2 caras basales planas, paralelas y congruentes, 1 cara lateral que es curva y 2 aristas basales.
Red del cilindro
Al abrir un cilindro y colocar todas las caras en un mismo plano, obtenemos su red. Así:
Puedes observar que en esta red se nos forma un rectángulo para la cara lateral, cuyos lados son el perímetro de las circunferencias que forman las bases.
La esfera
Es el cuerpo redondo que se genera al rotar un semicírculo alrededor de su diámetro.
Elementos de una esfera
- Generatriz: es la semicircunferencia que genera la superficie esférica
- Centro de la esfera: es el centro de la semicircunferencia y corresponde al punto O
- Radio de la esfera: es el radio de la semicircunferencia: OA
- Diámetro de la esfera: es el segmento que une 2 puntos opuestos de la superficie esférica, pasando por el centro: AB
Observa los elementos en este esquema:
La esfera tiene una sola cara curva.
Cortes
Una esfera puede ser cortada por un plano que pasa por su centro. De esta forma se obtienen 2 semiesferas y el plano deja como borde un círculo máximo.
Si el plano corta a la esfera sin pasar por su centro se obtienen 2 casquetes esféricos.